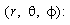|
Transforming geographic to geomagnetic coordinates
Figure B1 shows the geographic and geomagnetic coordinate systems. The position vector, rm, in the
geomagnetic coordinate system is related to the position vector, rg, in the geographic coordinate system
by a transformation:
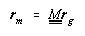
The transformation describes a latitudinal plus a longitudinal rotation: A rotation of the
coordinate axes by an angle, 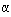 , from the geographic
pole along the Greenwich meridian (0 oE geographic).
That is, a rotation about the y-axis in Figure B1(a). Plus a rotation by an angle, , from the geographic
pole along the Greenwich meridian (0 oE geographic).
That is, a rotation about the y-axis in Figure B1(a). Plus a rotation by an angle, 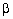 , in the geographic equatorial plane. That is, a rotation about the z-axis in Figure B1(a). Hence the
geographic coordinates of the geomagnetic North pole are ( (90-
, in the geographic equatorial plane. That is, a rotation about the z-axis in Figure B1(a). Hence the
geographic coordinates of the geomagnetic North pole are ( (90-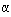 ) oN, ) oN,
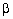 oE ). The matrix, oE ). The matrix, 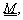 , is
then given by: , is
then given by:
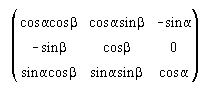
We express the Cartesian components (x, y, z) of the general position vector, r, in terms of
spherical polar coordinates 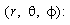
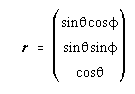
Substituting equation (B.2) for  and equation (B.3) for rm and
rg in equation (B.1) we can then solve for
geomagnetic co-latitude and longitude in terms geographic co-latitude and longitude.
We find: and equation (B.3) for rm and
rg in equation (B.1) we can then solve for
geomagnetic co-latitude and longitude in terms geographic co-latitude and longitude.
We find:
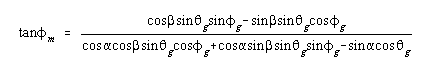
and
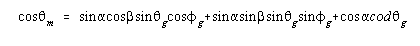
For example, using 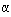 = 11.5o, = 11.5o,
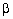 = -69.0o, the geographic
coordinates of Halley (-75.5 oN, -26.6 oE)
transform to the geomagnetic coordinates (-65.8 oN, 24.3 oE). = -69.0o, the geographic
coordinates of Halley (-75.5 oN, -26.6 oE)
transform to the geomagnetic coordinates (-65.8 oN, 24.3 oE).
|
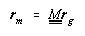
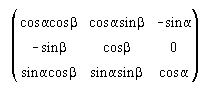
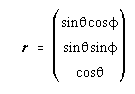
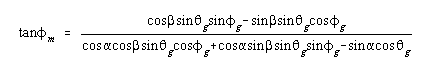
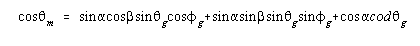
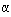 , from the geographic
pole along the Greenwich meridian (0 oE geographic).
That is, a rotation about the y-axis in Figure B1(a). Plus a rotation by an angle,
, from the geographic
pole along the Greenwich meridian (0 oE geographic).
That is, a rotation about the y-axis in Figure B1(a). Plus a rotation by an angle, 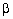 , in the geographic equatorial plane. That is, a rotation about the z-axis in Figure B1(a). Hence the
geographic coordinates of the geomagnetic North pole are ( (90-
, in the geographic equatorial plane. That is, a rotation about the z-axis in Figure B1(a). Hence the
geographic coordinates of the geomagnetic North pole are ( (90-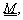 , is
then given by:
, is
then given by: